Правило наименьших издержек. Правило максимизации прибыли при использовании экономических ресурсов
В качестве исходного положения при анализе издержек производства был рассмотрен тезис о том, что в основе производства любого товара или услуги лежат затраты экономических ресурсов. В этой связи возникают вопросы:
• Как будет выглядеть условие максимизации прибыли фирмы, использующей некоторый ресурс R? При каких затратах этого ресурса (QR) прибыль фирмы будет максимальной?
• Если в производстве данного блага применяется несколько видов ресурсов — R1, R2, R3, ..., Rn-1,Rn, то каково должно быть их сочетание, чтобы обеспечить фирме возможность производить данную продукцию с наименьшими издержками?
• Каково должно быть сочетание R1, R2, R3, ..., Rn-1,Rn, чтобы фирма получила максимальную прибыль?
Любая фирма максимизирует прибыль, выпуская такой объем продукции, при котором получаемый ею предельный доход (MR) равен предельным издержкам (МС). Величины предельного дохода и предельных издержек находятся в зависимости от динамики валового дохода (TR) и валовых издержек (ТС) соответственно. Как изменяются TR и ТС при введении в производство дополнительной единицы ресурса? Введем два новых термина — «предельный продукт в денежном выражении» и «предельные издержки на ресурс».
Предельный продукт в денежном выражении (MRP) представляет собой изменение суммарной выручки (TR) фирмы за счет производства и реализации единиц товара, выпушенных при использовании каждой дополнительной единицы данного ресурса:
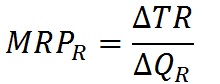 (1)
(1)
где QR — количество ресурса R, вовлеченного в производство данного блага (некоторого товара X).
Предельные издержки на ресурс (MPС) отражают изменение суммарных издержек фирмы (ТС) в связи с вовлечением в производство дополнительной единицы рассматриваемого ресурса:
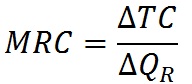 (2)
(2)
Любая фирма для максимизации прибыли должна использовать дополнительные единицы любого ресурса до тех пор, пока каждая последующая единица данного ресурса дает больший прирост общего дохода фирмы по сравнению с приростом ее валовых издержек. Тогда условием максимизации прибыли является применение такого количества данного ресурса, при котором предельный продукт в денежном выражении будет равен предельным издержкам на ресурс: MRP = MRC. Это тождество помимо логического обоснования объясняется и математически.
Итак, исходным условием нашего математического доказательства станет равенство MR = MС, составляющие которого рассчитываются следующим образом:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
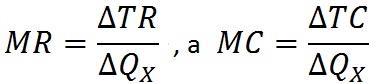
где ![]() QX — изменение объема производства некоторого товара X. Далее определяется показатель предельного продукта (MP):
QX — изменение объема производства некоторого товара X. Далее определяется показатель предельного продукта (MP):
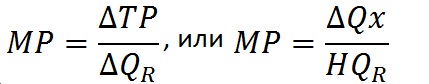
Теперь используем прием, распространенный в математике, — и числитель и знаменатель в выражениях mrp и MRC умножим на одну и ту же величину, а именно на ![]() Qx. Ясно, что частное от деления в формулах от таких преобразований не изменится. Получаем:
Qx. Ясно, что частное от деления в формулах от таких преобразований не изменится. Получаем:
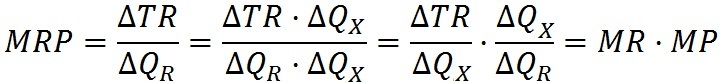 (3)
(3)
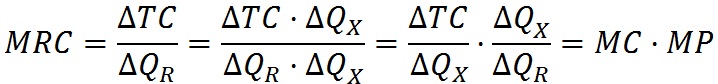 (4)
(4)
Таким образом, MRP= MR x MP, т. е. произведению предельного дохода фирмы и предельного продукта данной единицы ресурса, а предельные издержки на ресурс можно получить, умножая величину предельных издержек фирмы тоже на величину предельного продукта: MRC = МС x MP. В выражениях (3) и (4) вторые множители совпадают. С другой стороны, в начале нашего доказательства мы принимали MR = МС, что означает равенство и совпадение величин первых множителей в данных выражениях. Отсюда можно констатировать, что тождество MRP = MRC действительно отражает условие максимизации прибыли для предприятия-производителя.
Если фирма, использующая в производстве данный вид ресурса, не в состоянии влиять на его цену (т. е. покупает ресурсы на совершенно конкурентном рынке факторов производства), то величины предельных издержек на ресурс для всех нанимаемых единиц этого ресурса будут одинаковы и равны цене ресурса (РR). Условие максимизации прибыли в этом случае примет вид: MRP = MRC - PR, или MRP = PR. Значимость приведенных здесь положений проявится при анализе спроса на экономический ресурс.
Представленные выше положения справедливы в отношении отдельного ресурса. Однако издержки производства фирмы включают в себя затраты на привлечение множества видов ресурсов, без использования которых невозможно осуществить производство. В качестве инструмента анализа этого вопроса экономическая наука использует понятие «производственная функция». Производственная функция отражает зависимость между некоторым объемом произведенной продукции (Qx) и количественными затратами ресурсов (QR1, QR2,QR3, ..., QR(n-1),QR(n)), требующимися для создания этого товара X: Qx=f (QR1, QR2,QR3, ..., QR(n-1),QR(n))
Любая производственная функция отражает конкретную технологию, показывая, какой вклад в создание готовой продукции вносит каждый из ресурсов, вовлеченный в производственный процесс. С помощью производственной функции можно определить максимально возможный выпуск продукции при заданных затратах ресурсов. С другой стороны, она позволяет выяснить, каково минимально необходимое количество ресурсов для производства заданного объема продукции. Производственная функция помогает определить различные комбинации применяемых ресурсов, обеспечивающих возможность достижения одного и того же результата, т. е. одной и той же величины Qx. В этой связи возникают два основных вопроса: каким должно быть сочетание ресурсов для производства любого данного уровня объема продукции с наименьшими вздержками и какое сочетание ресурсов будет максимизировать прибыль фирмы?
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Для ответа на первый вопрос вспомним, что в качестве основного показателя эффективности применения любого ресурса мы рассматриваем уровень его производительности, в частности показатель MP. В количественном отношении эффективность использования любого ресурса определяется не только его предельной производительностью, но и рыночной ценой этого фактора производства (PR) и будет описываться выражением: MPi/PRi , где МРi — предельный продукт i-го ресурса; РRi — его цена.
Любая фирма при этом будет всегда отдавать предпочтение тому ресурсу, для которого соотношение MP и РR будет выше,. Вовлекая все большее количество данного ресурса в производственный процесс, фирма столкнется с проблемой снижения эффективности его использования, при неизменности цены ресурса, в силу действия закона убывающей предельной производительности; его mp начнет сокращаться, а значит, частное от деления MP/PR тоже будет уменьшаться. Очевидно, что фирма будет продолжать увеличивать объемы применения рассматриваемого ресурса только до тех пор, пока его относительная эффективность не сравняется с относительной эффективностью других ресурсов, т.е. пока не будет выполняться равенство
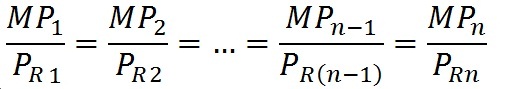 (5)
(5)
Иными словами, издержки на производство любого объема продукции минимизируются, если предельный продукт на каждую денежную единицу стоимости каждого применяемого ресурса будет одинаковым. Этот принцип получил название правила наименьших издержек.
Представленное тождество (5) позволяет найти такую комбинацию ресурсов, которая обеспечит фирме производство заданного объема продукции с минимальными издержками, но не гарантирует получение максимальной прибыли. Выше было доказано, что фирма максимизирует прибыль при соблюдения равенства mrp = mrС. Если фирма использует всего два ресурса — А и В, максимальная прибыль достигается, если: MRPA = MRCA а MRPB = MRCB, т.е. когда
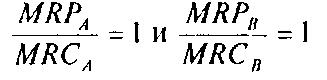
Иными словами, когда имеет место следующее выражение:

Если фирма не в состоянии влиять на цены экономических ресурсов и каждую следующую единицу ресурса вынуждена приобретать по сложившейся на рынке цене (pr), то mrc = PR, и приведенное выше условие трансформируется:
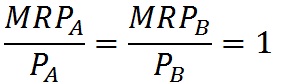
где РА и Рв — соответственно цены ресурсов А и В.
В этом примере рассмотрена ситуация для двух видов ресурсов. Если полученные результаты исследования «расширить» для всех ресурсов, применяемых фирмой, получим следующее выражение, названное правилом максимизации прибыли:
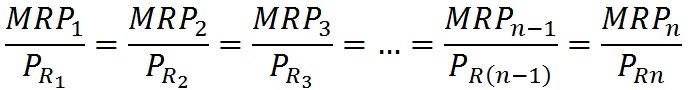 (6)
(6)
Данное уравнение характеризует ситуацию, когда фирма не только минимизирует издержки, но и максимизирует прибыль. По своей форме оно более строгое, чем тождество (5), и требует не просто пропорциональности предельного продукта и цены ресурса, а равенства числителя и знаменателя.
